3 - Expliquer l'apprentissage automatique
Dans la partie précédente, nous avons évoqué différents types d’opacité. Les deux premières étaient liées au secret des entreprises et aux limites de connaissance informatique de la population. Nous laisserons ces deux cas de coté. Nous nous plaçons dans le cadre du dernier type d’opacité, le cadre d’un algorithme dont l’opacité serait uniquement liée à sa manière d’opérer. Plusieurs questions vont donc se poser. En effet, expliquer le fonctionnement de l’algorithme va dépendre du public de destination et de la visée. Nous allons donc explorer les objets, modes et moment de visualisation d’un algorithme d’apprentissage automatique. Nous choisissons de focaliser l’étude sur les réseaux de neurones convolutionnels.
Que représenter ?
Comme vu dans les pages précédentes, une visualisation commence toujours par l’acquisition de données. Nous pouvons ainsi distinguer quatre grands aspects visualisable d’un réseau de neurones1 en fonction des données qu’ils génèrent :
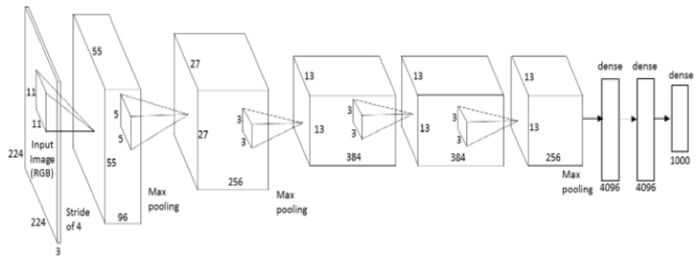
Figure 1 : Schéma d’un réseau de neurones convolutionnels avec figuration des aspects visualisables
-
Architecture du modèle : L’architecture du modèle peut tout d’abord être représentée. Celle-ci permet de représenter comment les données se propagent dans le modèle. Cette représentation peut inclure la représentation des liens au matériel ainsi qu’aux sauvegardes et logs effectués.
-
Paramètres appris : Les paramètres appris lors de l’entrainement peuvent être représentés. Les poids des neurones peuvent être comparés de même que l’évolution des filtres de convolution.
-
Étapes du processus : Au cours des passes avant et retour d’un réseau de neurones, certains évènements peuvent être visualisés. La valeur d’activation de chaque noeud du réseau peut permettre d’évaluer le “niveau d’utilisation” d’un neurone. Le processus de rétro-propagation peut être visualisé à chaque couche du réseau pour montrer comment l’erreur est distribuée sur les paramètres du réseau.
-
Les données aggrégées : Enfin, des données aggrégées peuvent être obtenues, particulièrement lors de l’entrainement, comme les valeurs de perte ou la précision de prédiction des classes au fil des epochs. Ces données sont généralement représentées en fonction du temps afin d’évaluer l’avancement de l’entraînement. Ces données sont particulièrement intéressantes car elles permettent de comparer des modèles très différents.
Quand ?
Dans le cadre d’un algorithme d’apprentissage automatique, se pose la question du moment de la représentation, pendant ou après l’entrainement. Ainsi, dans le cas d’un réseau de neurones1 :
-
Pendant l’entraînement : Visualiser un modèle pendant l’entrainement permet d’observer l’évolution de sa performance et potentiellement détecter des problèmes comme l’overfitting. Ces visualisations peuvent ainsi permettre de gagner du temps en arrêtant des entrainements qui ne mèneraient à rien.
-
Après l’entraînement : Visualiser les sorties du système, les features apprises ou l’état final des poids. Cela permet en particulier de comparer différents modèles sur lesquels les hyperparamètres ont varié.
Comment ?
Node-link diagrams
Une première idée de représentation des réseaux de neurones est la visualisation par noeuds et liens. Cela permet de montrer comment sont reliés les neurones et la manière dont ils s’influencent. Les visualisations les plus simples sont statiques et utilisent la couleur et l’épaisseur des liens pour encoder des valeur d’activation et l’influence de certains neurones.
Dans la représentation ci-dessous, un réseau de neurones simple, avec une couche cachée est visualisée. Il est destiné à repérer l’appartenance d’un pixel au cerveau sur une IRM.
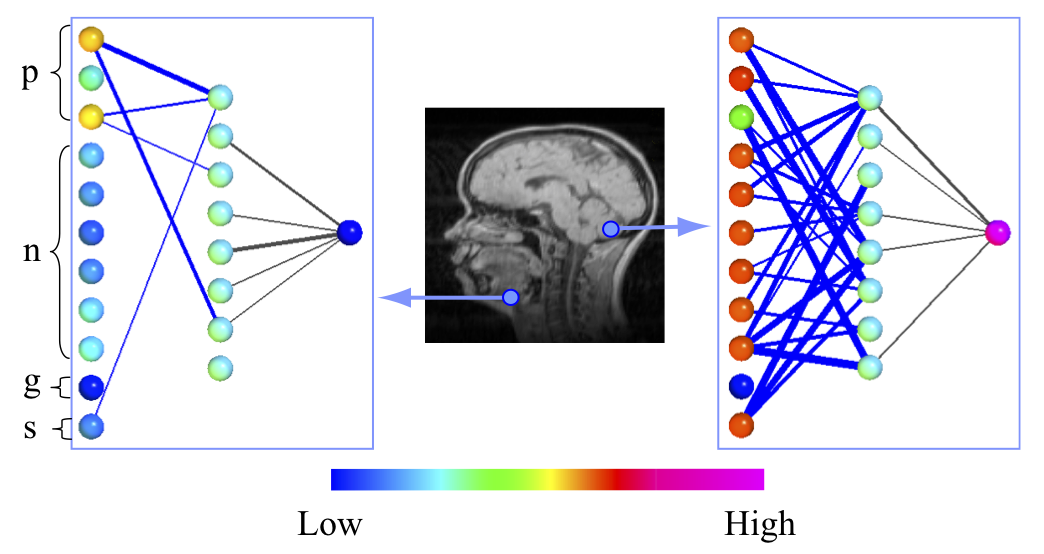
Figure 2 : Visualisation des valeurs des neurones d’entrée et de sortie pour une classification du cerveau sur une IRM. p correspond aux position (x,y,z), n à des informations sur les pixels environnants, g et s sont des paramètres d’IRM.2
Il est remarquable que les entrées n’aient pas la même influence sur le résultat final en fonction de la position du pixel analysé. En effet, le système n’utilise que les informations de position pour prédire le résultat d’un pixel situé au niveau de la machoire. Au contraire, un pixel dans le cerveau utilisera presque toutes les informations disponibles pour valider le résultat.
Cependant, la visualisation, par sa staticité, devient difficile à exploiter pour un réseau de neurones plus complexe. D’autres visualisation s’intéressent au contraire à rendre explorable le réseau afin de laisser l’utilisateur adapter la densité visuelle d’information présentée.
L’outil TensorBoard, permet de représenter un réseau implémenté en TensorFlow. La représentation est toujours faite de noeuds et de liens, mais elle permet d’explorer le réseau et d’agrandir le niveau de détails sur certains noeuds.
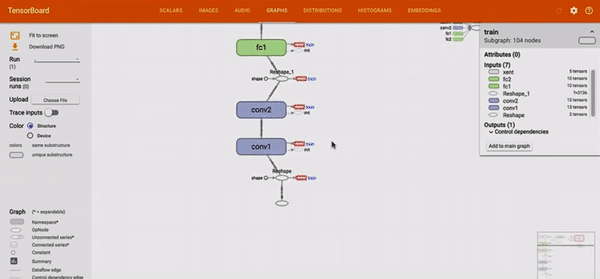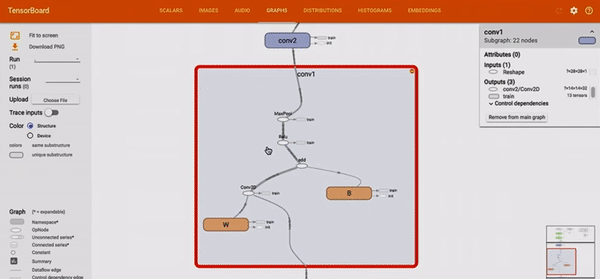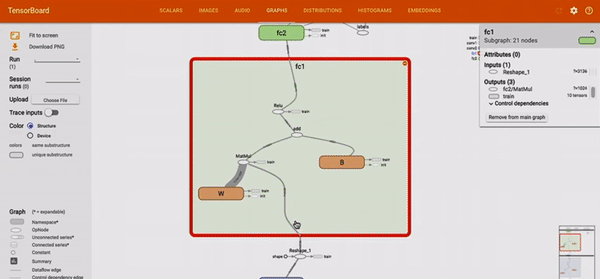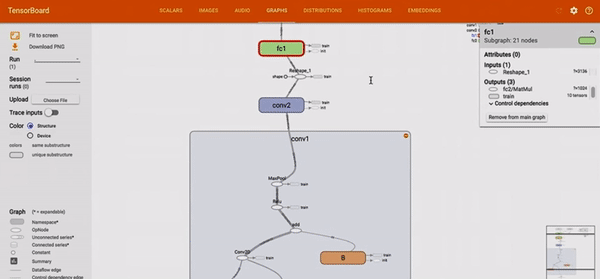
Figure 3 : Démonstration des possibilités d’exploration au sein d’un node-link diagram sur l’outil TensorBoard.3
Nuages de points
Les données d’entrée d’un réseau de neurones sont très variables et sont généralement représentées par des objets à grande dimension. Ces grandes dimensions sont un réel défi pour la visualisation de données. En effet, comment comparer le traitement d’un modèle sur des entrées différentes en plaçant sur un même graphique les entrées et les résultats. Face à ce problème de dimension, un solution courante existe, la projection. Nous représentons dans le schéma suivant l’utilisation d’une projection pour comparer la bonne classification d’image de 32x32 = 1024 pixels.
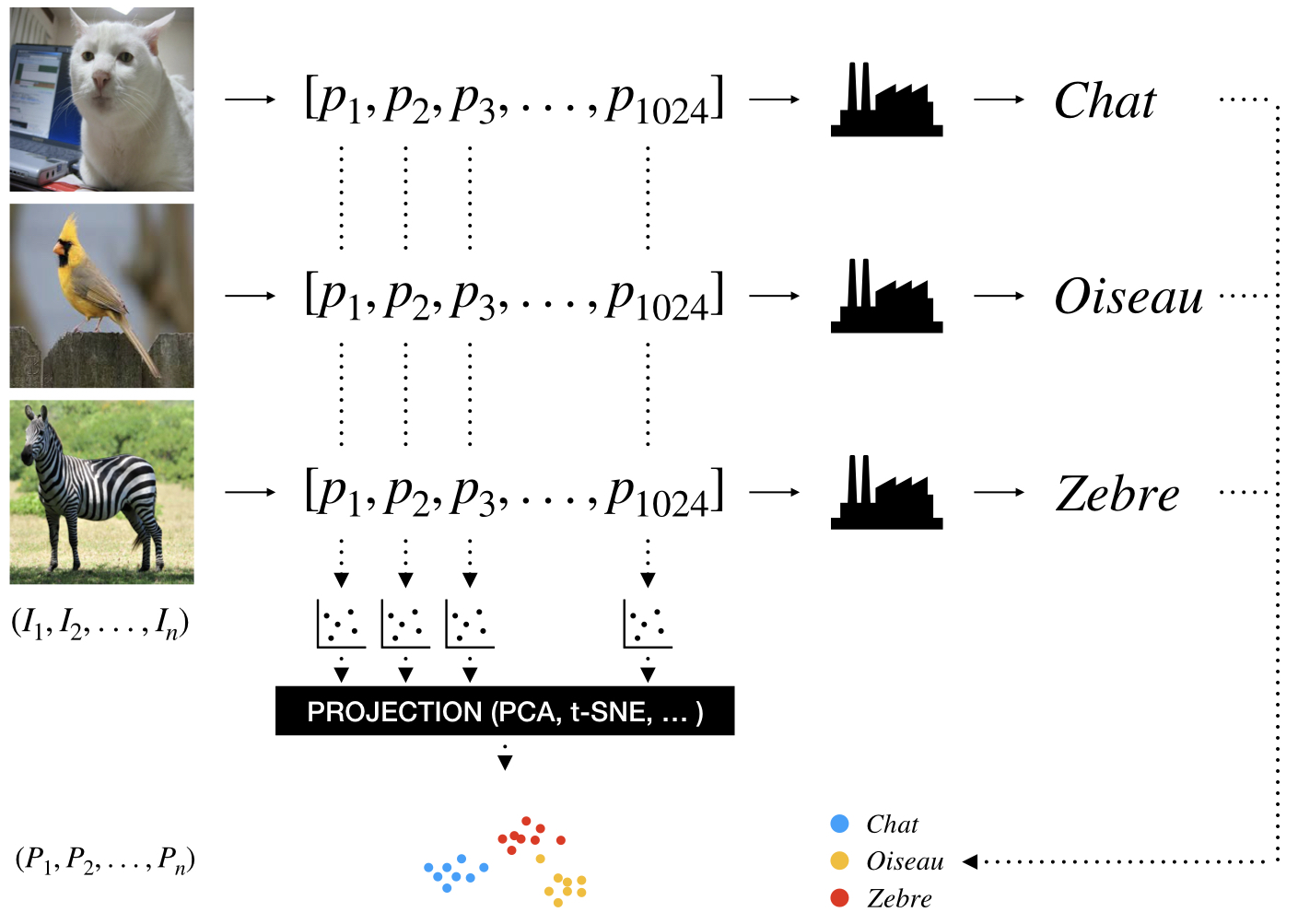
Figure 4 : Schématisation d’une réduction de dimension
Chaque image est représentée par un vecteur de 1024 pixels. Il serait possible d’effectuer 1024 représentations des pixels entre les images d’entrée. Néanmoins, cela ne permettrait pas de donner une idée de la qualité du modèle. Une projection des 1024 dimensions en 2D ou 3D est donc effectuée permettant de placer chaque image d’entrée dans un nuage de point (scatter plot). À noter que les axes après projection n’ont pas toujours une signification particulière. Les sorties correspondant à des classes sont elles encodées simplement par des couleurs.
Le choix de projection est à la discretion de l’équipe développant le modèle. Néanmoins, certaines projections seront mieux adaptées en fonction de des distributions des données d’entrée.4 Ci-dessous quelques exemples de représentations après projection pour la prédiction de nombres écrits à la main provenant de la base MNIST.
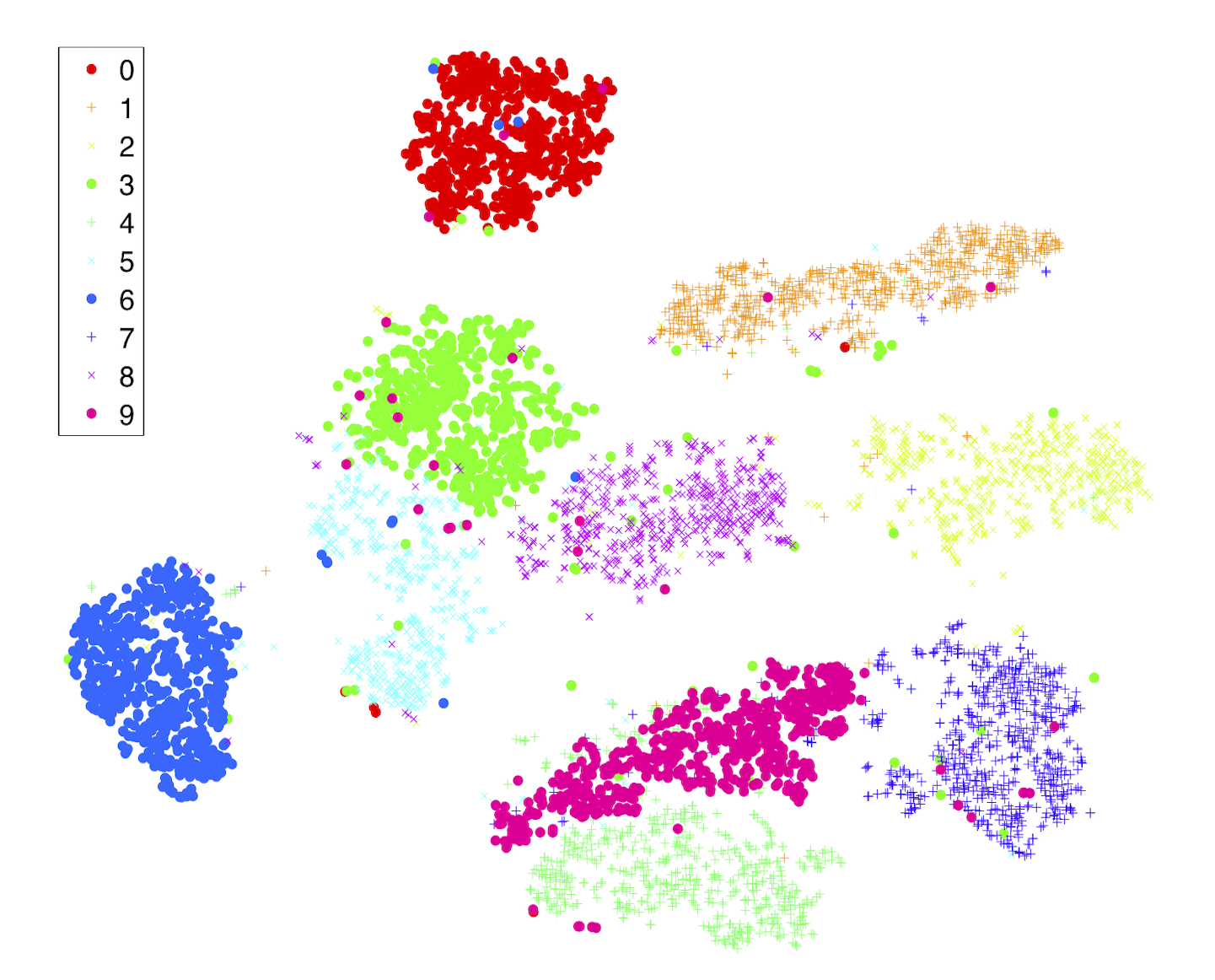
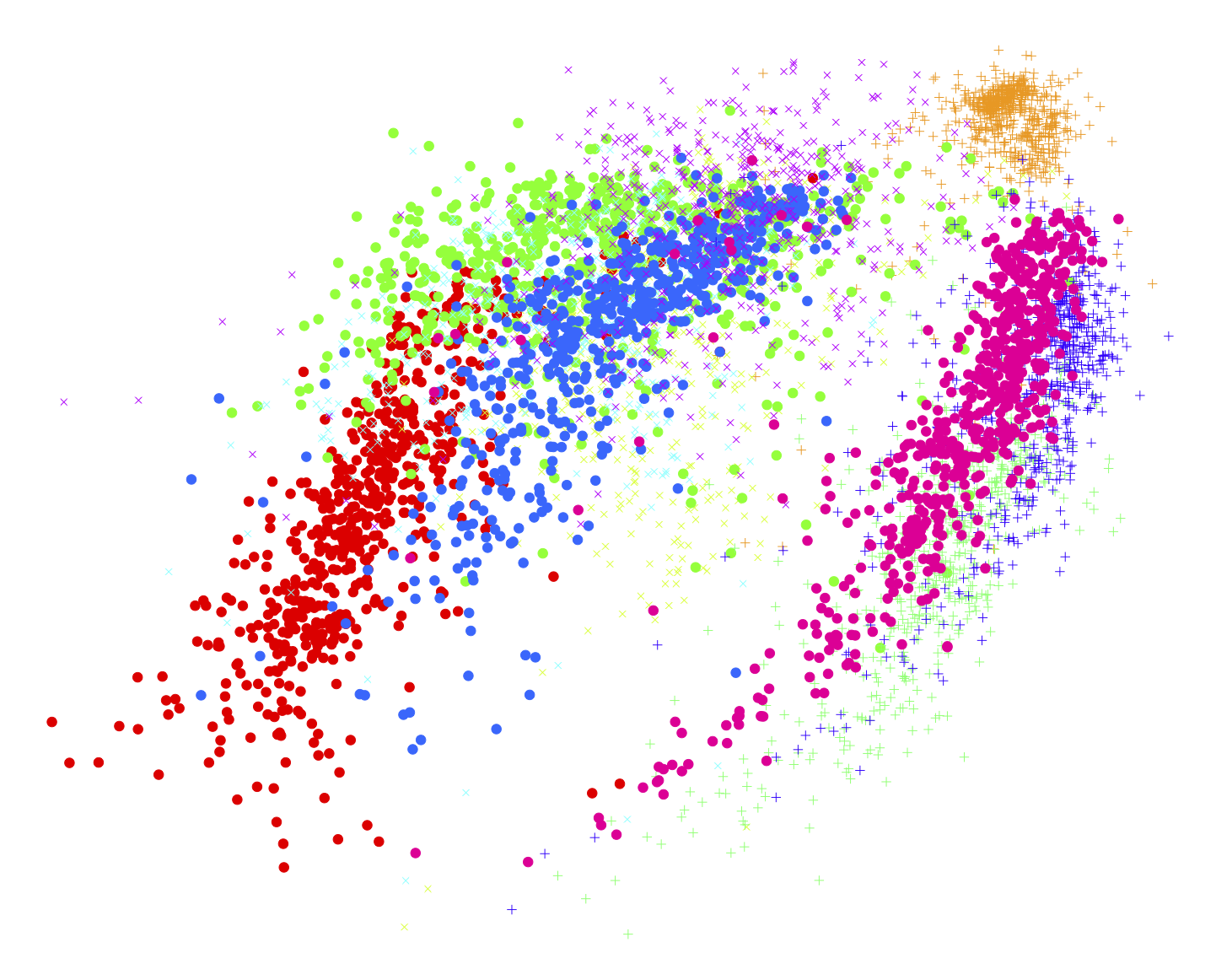
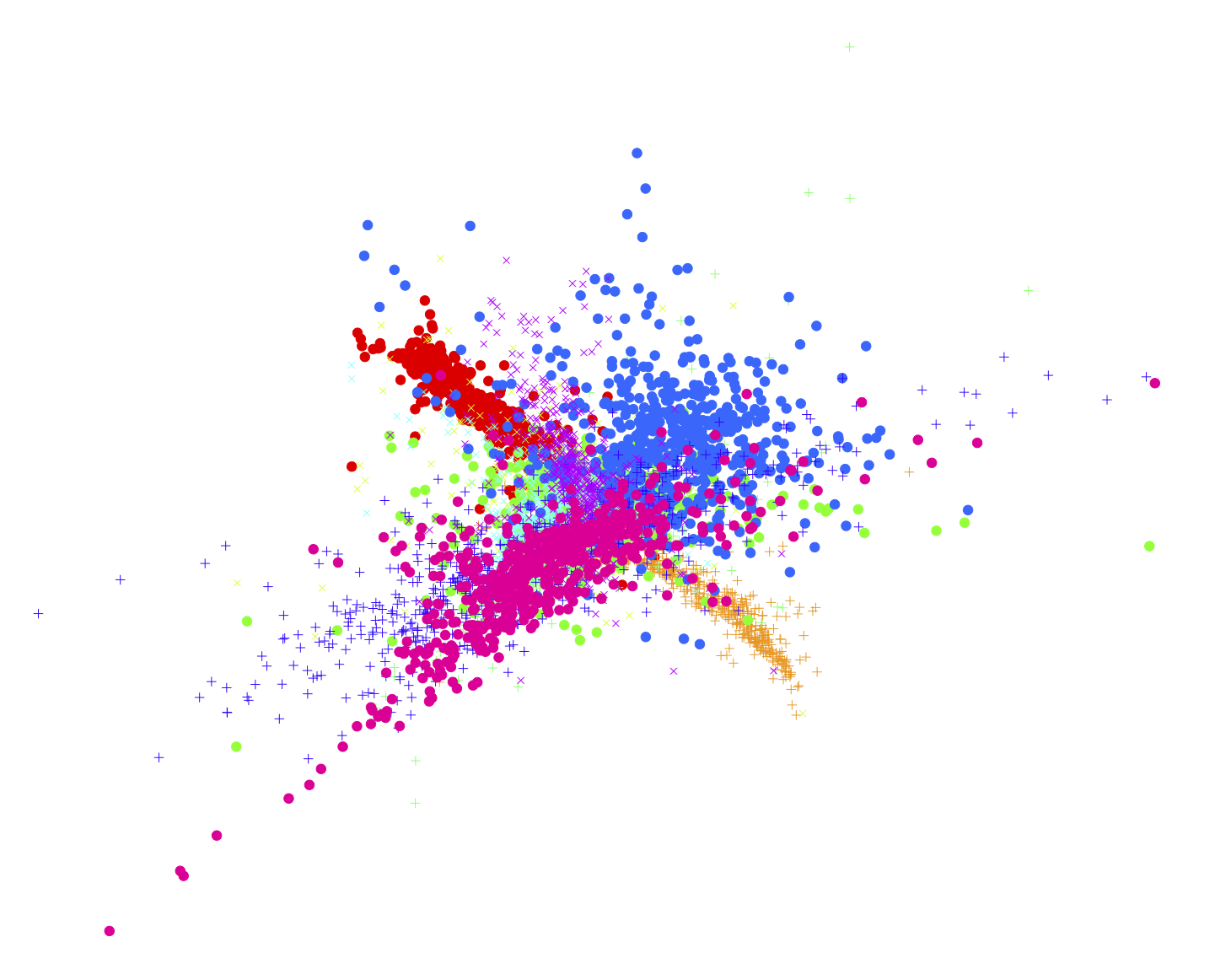
Figure 5 : Représentation des projections (t-SNE, Isomap, LLE) des entrées de MNIST et de leur résultat4
À noter que les sorties représentées peuvent être autres que les valeurs de classification finales. Des valeurs d’activation, internes au réseau, peuvent ainsi être représentées.
Lignes et surfaces
La phase d’entrainement des algorithmes d’apprentissage automatique est la plus longue et consommatrice d’énergie. Ainsi, en vue d’optimiser leurs recherches, les développeurs de modèles essaient de suivre en temps réel la performance du modèle. Des visualisations simples en courbes (line charts) ou en surface se sont imposées. Ces représentations aident plus particulièrement à comprendre le fonctionnement de la rétro-propagation.
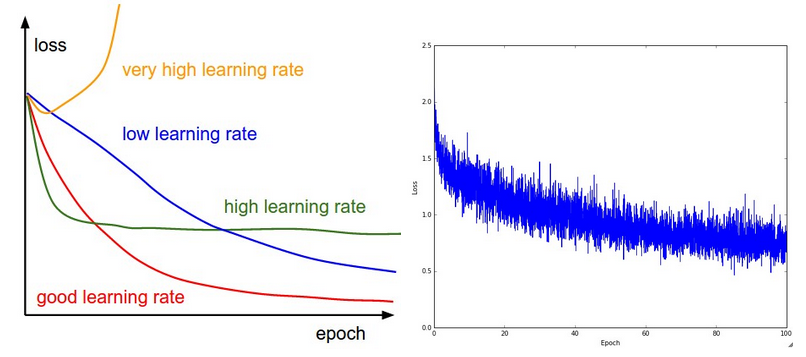
Figure 6 : Représentation d’évolutions caractéristiques de fonctions de perte et un exemple réel.5
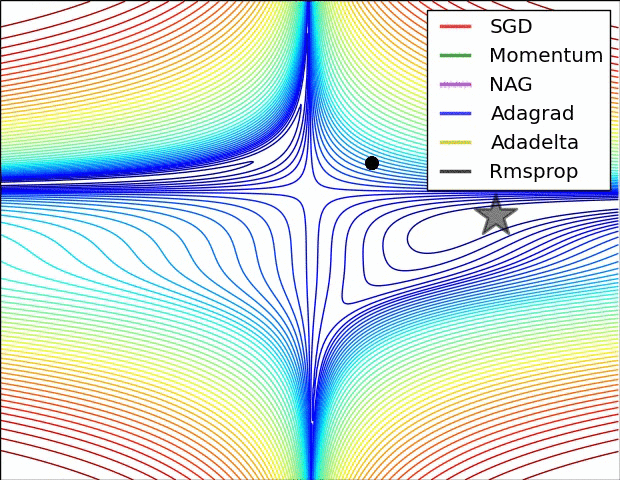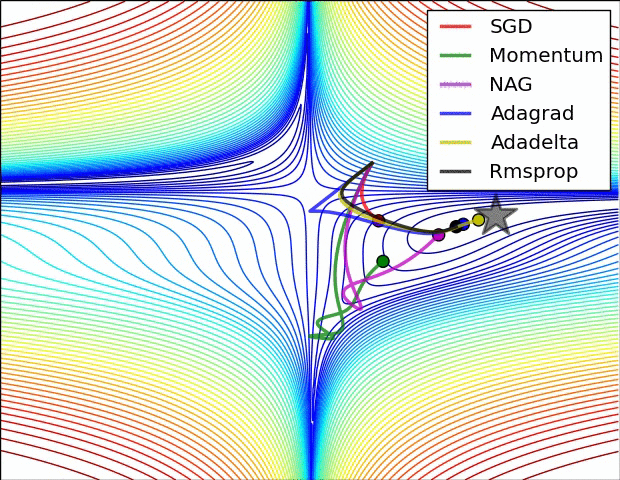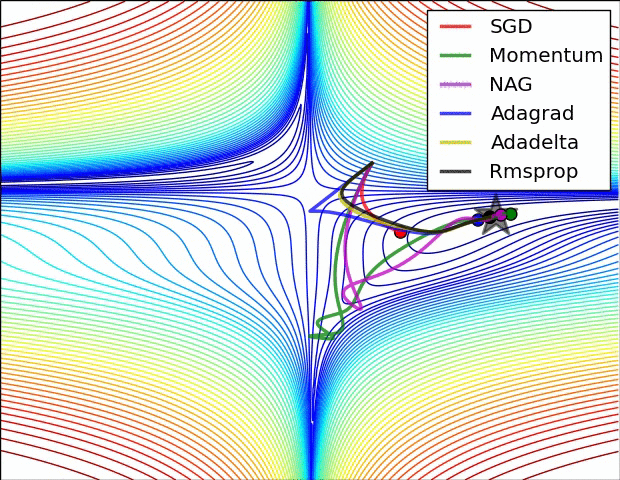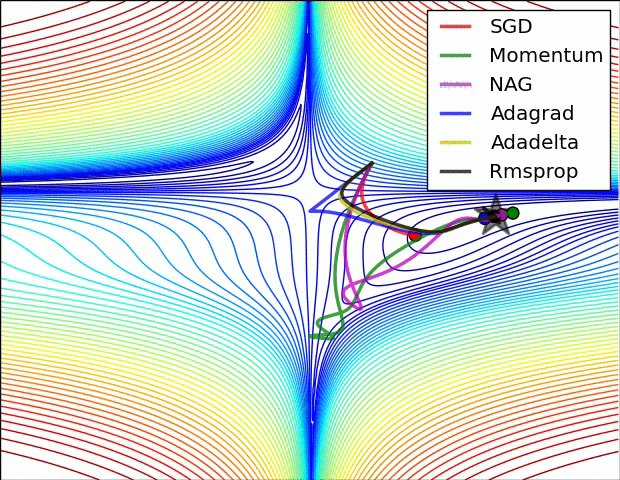
Figure 7 : Représentation en surface d’algorithmes d’optimisation5
Cela peut même aller jusqu’à la représentation en 3D.

Figure 8 : Représentation en surface de la perte associée à des modèles différents 6
Ces représentations ont de nombreux avantages.
- Elles reposent sur des données agrégées facile à générer
- Elles sont générallement simples à lire
- Elles permettent de comparer des modèles similaires se différenciant par leurs hyperparamètres ou même des modèles très différents.
Visualiser l’apprentissage du modèle
Une fois un modèle entrainé et donnant des résultats satisfaisants, il est logique de se demander ce qu’il sait. En effet, il est en mesure de classer correctement des entrées cependant des questions se posent sur les aspects des entrées qui lui sont vraiment utiles et la “compréhension” qu’il a des classes. Deux types de visualisations particulières existent pour cela dans le cas d’images en entrée.
- Attribution : Ce type de visualisation permet, pour une image d’entrée, de générer une image d’entrée modifiée en faisant dire au modèle les zones qui lui ont permis de faire sa classification. Ces images générées sont souvent appelées “saliency maps” ou carte des saillances.

Figure 9 : Exemples de saliency maps7
- Visualisation de classe : Ce type de visualisation permet de générer une image artificielle représentant une classe. Ainsi, il devient possible de voir ce que le modèle considère comme une classe donnée. Il est particulièrement intéressant de comparer sa représentation d’une classe à une autre.

Figure 10 : Exemples de visualisations de classes7
Représentations mixtes intéractives
Pour terminer, de nombreuses représentations mixtes intéractives existent autour des réseaux de neurones. Ces dernières ont soit une visée ludique, soit une visée de tableau de bord. Les outils suivants sont particulièrement remarquables.
TensorSpace.js et le projet d’Adam Harley permettent l’exploration en 3D de réseaux de neurones convolutionnels.

Figure 11 : Exemple d’exploration de LeNet permise par TensorSpace.js8
ConvNetJS donne un tableau de bord de l’entrainement de réseaux de neurones dans des cas classiques comme MNIST ou CIFAR-10. Ce dernier exemple agrège différentes visualisations évoquées plus haut.
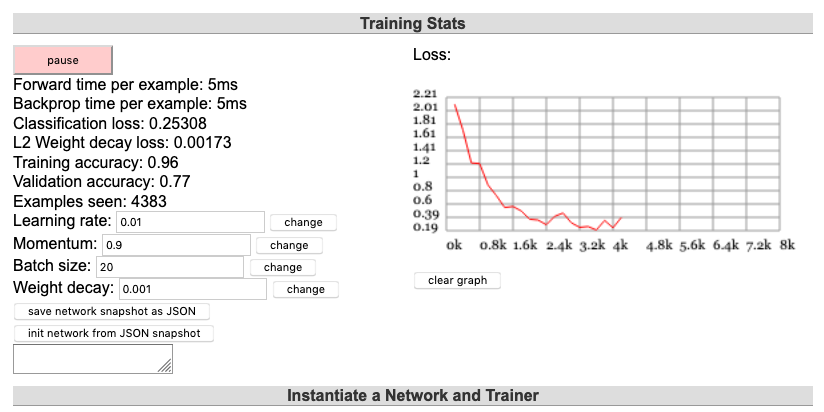
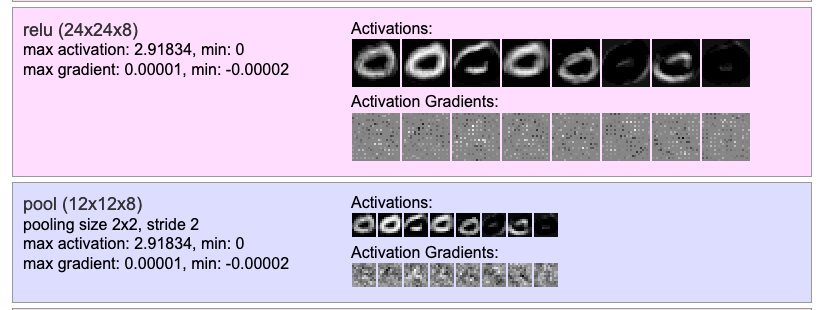
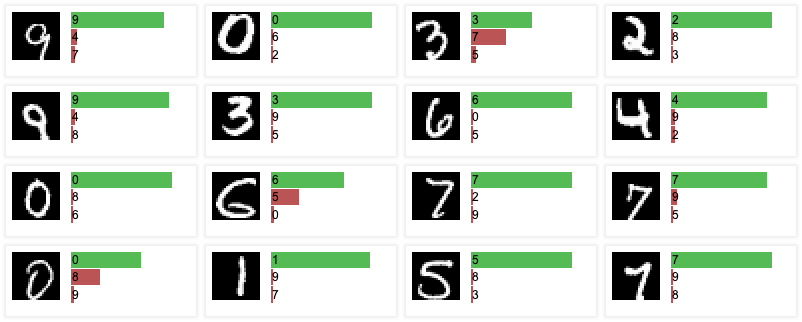
Figure 12 : Exemples de représentations figurants dans l’outil ConvNet 9
Bilan
Voici sous forme d’un tableau le résumé des représentations évoquées plus haut :
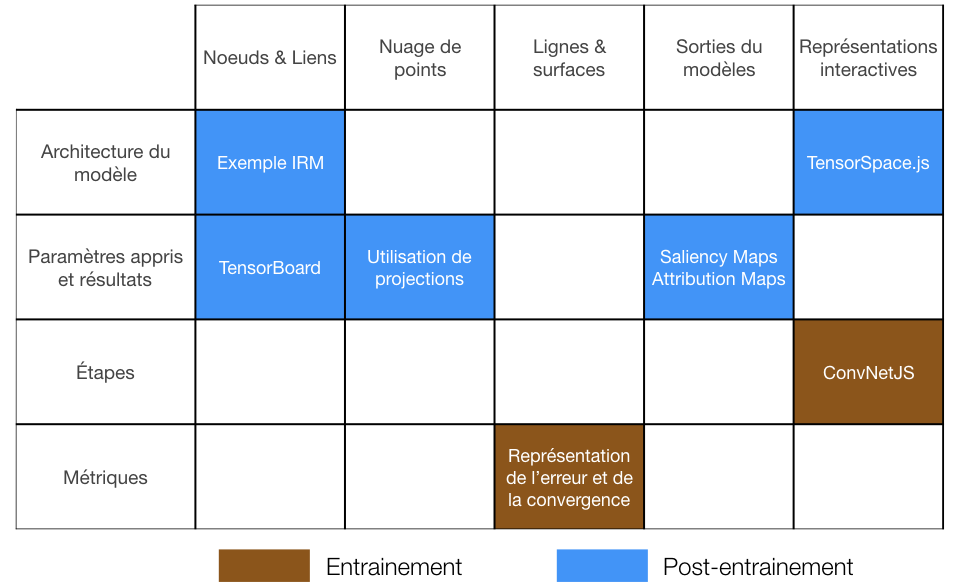
Figure 11 : Tableau bilan des solutions évoquées
Références
-
Fred Hohman, Minsuk Kahng, Robert Pienta, Duen Horng Chau, Visual Analytics in Deep Learning:An Interrogative Survey for the Next Frontiers, 2018 ↩ ↩2
-
Fan-Yin Tzeng, Kwan-Liu Ma, Opening the Black Box — Data Driven Visualization of Neural Networks ↩
-
Vidéo, Hands-on TensorBoard ↩
-
Laurens van der Maaten, Geoffrey Hinton VisualizingDatausingt-SNE, 2008 ↩ ↩2
-
Cours Stanford CS, CS231n Convolutional Neural Networks for Visual Recognition ↩ ↩2
-
Karen Simonyan, Andrea Vedaldi, Andrew Zisserman, Deep Inside Convolutional Networks: VisualisingImage Classification Models and Saliency Maps, 2014 ↩ ↩2