1 - Visualiser un algorithme
Il est difficile de visualiser
La force de la visualisation de données réside dans la communication de connaissance par encodage visuel afin de transformer des données abstraites en des représentations pertinentes. 1 Une visualisation réussie s’accompagne généralement d’un difficile travail de représentation. En effet toute visualisation nécessite de “composer avec une multitude de processus cognitifs et perceptifs” afin de s’adapter aux capacités du public et retenir sont attention2. Par ailleurs de réels difficultés techniques existent. Cela va de l’acquisition de données exploitables à la conception même des représentations avec outils informatisés.
Algorithmes en boites
La classification suivante3 a été proposée par Mike Bostock, le créateur de D3.js, l’un des outils le plus avancé de visualisation de données. Elle distingue trois familles d’algorithmes en fonction de leur opacité et leur associe trois couleurs.
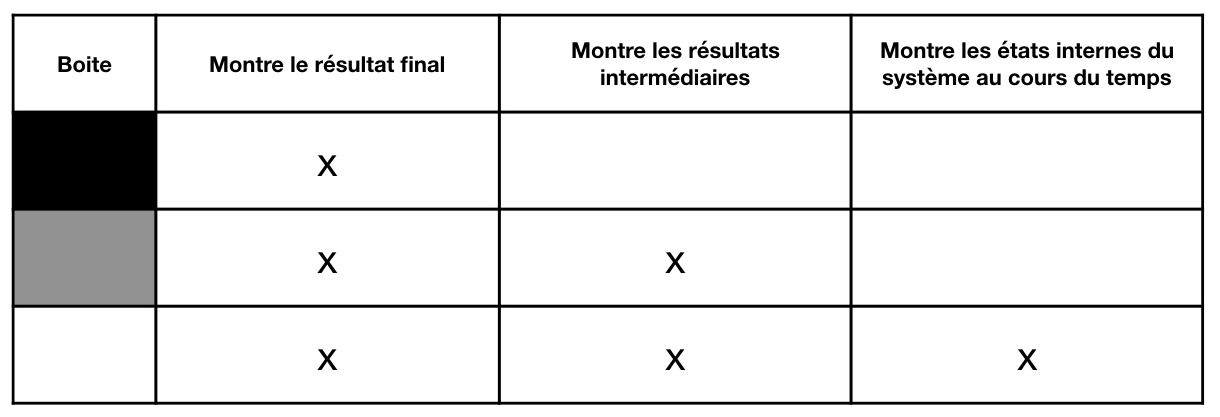
Figure 1 : Algorithmes classés en boites et ce que leur visualisation permet.
Une boite noire permet d’évaluer la véracité des résultats de l’algorithme mais sont fonctionnement est totalement opaque. Une boite grise donne une idée du comportement de l’algorithme mais peut induire en erreur ou apporter plus de questions que de réponses. La boite blanche enfin, a l’avantage de potentiellement expliquer le fonctionnement de l’algorithme. Cependant, la boite blanche s’accompagne d’une complexité plus grande d’information, liée au nombre et aux relations entre les données.3 Il est aisé de se représenter les trois situations précédentes avec un exemple simple d’algorithme : le calcul du PGCD par l’algorithme d’Euclide.
Exemple : calcul du PGCD par algorithme d’Euclide
Nous souhaitons illustrer la partie précédente avec un exemple connu de tous. L’algorithme étudié est l’algorithme d’Euclide permettant de déterminer le plus grand commun diviseur entre deux nombres entiers positifs. Cet algorithme peut facilement être implémenté avec un langage informatique. Nous choisissons de montrer ce que l’algorithme d’Euclide nous dit, traité comme une boite noire, grise ou blanche.
Les deux premiers exemples sont l’algorithme en version boite noire et grise. Dans le cas de la boite noire, le résultat final est bien connu, 2 est bien le PGCD de 72 et 26. Nous pouvons vérifier que l’algorithme fonctionne sur ce cas mais rien ne nous dit que l’algorithme fonctionnera sur d’autres car on ne peut dire ce qu’il s’y passe. Dans le cas de la boite grise, les valeurs successives de b sont renvoyées par le programme. Les valeurs sont rassurantes car elles permettent de voir que les étapes de l’algorithme implémenté sont bien conformes à la manière dont procèderait un humain. Cependant rien de m’assure que les résultats donnés par l’algorithme proviennent bien de divisions euclidiennes successives.
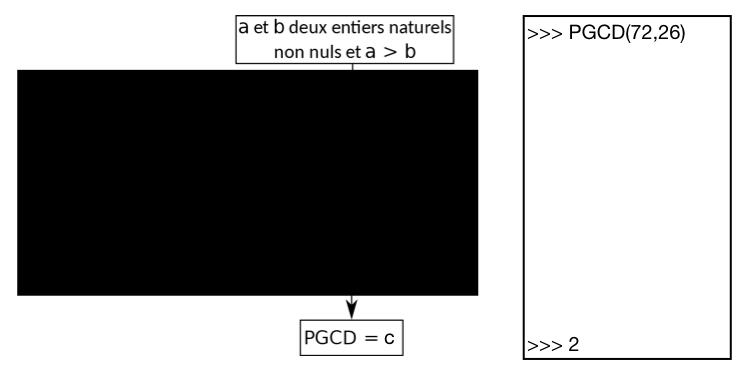
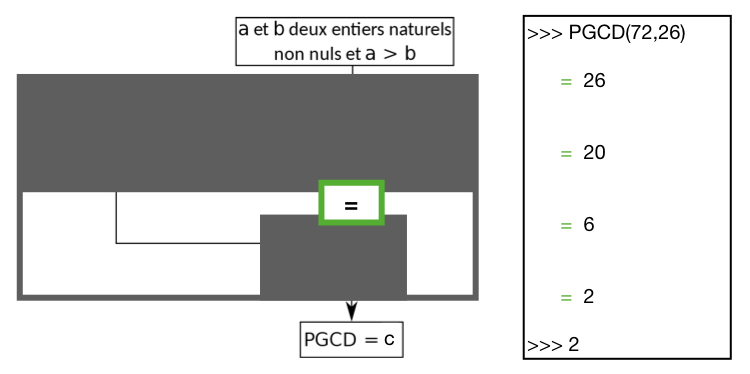
Figure 2 : Une boite noire et une boite grise pour l’algorithme de calcul du PGCD d’Euclide.
Enfin, l’algorithme en boite blanche permet de s’assurer de la bonne implémentation de l’algorithme. Il est alors possible de suivre chaque étape du programme et d’en comprendre la logique.
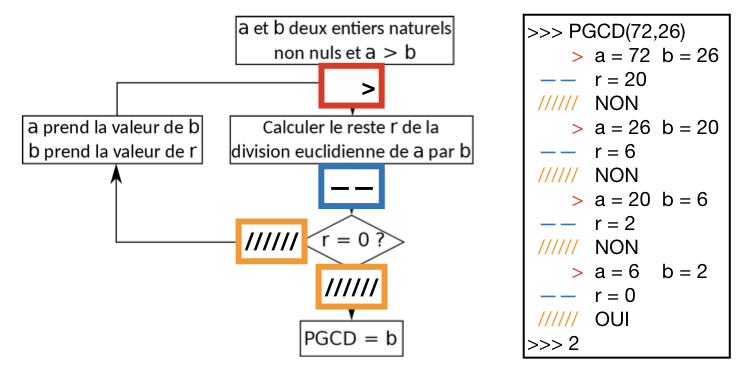
Figure 3 : Une boite blanche pour l’algorithme de calcul du PGCD d’Euclide.
Cependant, les données renvoyées par l’algorithme en version boite blanche ne constituent pas de l’information. Nous devons lier ces données à des représentations afin de créer une visualisation du fonctionnement de l’algorithme. Cette partie est la plus difficile. En effet, le cas d’une boite blanche soulève de nombreuses questions :
- Quelles données représenter ? Beaucoup de données sont renvoyées, toutes ne doivent pas être utilisées pour la visualisation sous peine d’obscurcir le sens de la visualisation.
- Comment encoder visuellement l’information ? Notre cas demande de représenter des nombres, ils peuvent correspondre à une longueur, une aire, une couleur, un symbole, …
- Que signifient les données ? Dans notre cas, la réponse est simple, mais ce n’est pas toujours le cas pour les algorithmes d’apprentissage automatique.
- Comment représenter le passage des étapes ?
- Ma visualisation fonctionnera t-elle si les données d’entrée changent ?
Nous proposons la visualisation suivante pour l’algorithme d’Euclide, avec 72 et 26 en entrées :

Figure 4 : Proposition de visualisation pour l’algorithme d’Euclide.
Nous espérons que cette première partie permet de montrer qu’il n’y a rien d’évident à visualiser un algorithme. Le cas traité est un cas facile comparé à d’autres algorithmes et en particulier à ceux d’apprentissage automatique. En effet, l’algorithme d’euclide implémenté est une transcription à l’identique d’une programme fait à la main. Autrement dit, nous savons résoudre le problème du PGCD sans ordinateurs. Il existe une autre classe d’algorithmes moins conventionnels qui nous aident à répondre à des problèmes que nous ne savons pas résoudre, les algorithmes d’apprentissage automatique.
Partie 2 : Pourquoi visualiser les algorithmes d’apprentissage automatique ?
Références
-
Fred Hohman, Minsuk Kahng, Robert Pienta, Duen Horng Chau, Visual Analytics in Deep Learning:An Interrogative Survey for the Next Frontiers, 2018 ↩
-
Isabel Meirelles, Design de l’information (traduction), 2013, ISBN 9791026100317 ↩
-
Mike Bostock, Visualizing Algorithms, 2014 ↩ ↩2